Luke DiPerna

Data guy. Father. Isotropic Gaussian Blob.

primes-splash

This is a classic coding problem that provides a lot of opportunity for creativity and ingenuity, in part because there are a number of ways to approach the problem. As is often the case, there are also a lot of small optimizations that can be found depending on what you are prioritizing. Today I want to look at a few ways to approach this problem, ending with a look at a special method I have always found fascinating: the Sieve of Eratosthenes.

Before we jump into the code, a quick mathematics refresher: what is a prime number? A prime number is a whole number greater than 1 that is not a product of two smaller whole numbers. Alternatively, it is a number that is only cleanly divisible by itself and 1. Any whole number greater than 1 that is not a prime number is a composite number. So the first challenge will be to determine whether a given number is prime or composite.

For my first attempt, I kept things basic. The function below takes a given object (x) and checks if it is an integer. If so, it checks if it is greater than 2. Then, it attempts to divide that number by each integer between 2 and x. If any of the results are a whole number, then x is a composite, not a prime.

def is_prime(x):
  # check for integer greater than 2
  if type(x) != int or x<2:
      return False  

for n in list(range(2, x)):
  # modulo returns the remainder after division
  if  x%n == 0:
    return False

return True

The above function gets the job done, though it is far from the most efficient code ever written. Let’s see the output below:

for x in list(range(1, 6)):
  print(f'{x} is prime: {is_prime(x)}')

Output:

1 is prime: False
2 is prime: True
3 is prime: True
4 is prime: False
5 is prime: True

It works, but how can we improve it? One way would be to increase the speed. For small numbers the computing time is negligible, but for larger numbers, the function is dividing x by every smaller integer. Another way to put this is that x is divided x-2 times. This means if x=100, then the function is performing division 98 times. Can this be reduced? Absolutely.

To think about how we can reduce the number of calculations, let’s use x=16 as an example. To find if it is a prime, we are currently dividing 16 by each number from 2-15. Since 16 is not a prime, we know that at least one combination of whole numbers can be multiplied to equal 16, but what are the combinations? Let’s check each possibility by hand:

2 * 8 = 16
3
4 * 4 = 16
5
6
7
8 * 2 = 16
.
.
.
15

Do we really need to check that many combinations? For even numbers, it does not matter since the function stops running after the first attempt to divide by 2. For example: 16/2=8, so we immediately know 16 is not prime. But if the number is prime, the current function still has to check every smaller whole number before it can make the determination of prime or composite.

Looking at the example above, however, demonstrates that we don’t actually need to check every single combination. As we can see, 2*8 and 8*2 both equal 16. We only find unique product pairs up to 4 (2*8 and 4*4). What about if x=36? In this case, the product pairs are:

2 * 18
3 * 12
4 * 9
—
6 * 6
—
9 * 4
12 * 3
18 * 2

This time we see that there are no unique pairs after n=6. Do you see the connection yet? In each case, we only need to check each whole number up to \(\sqrt{x}\). So when x=16, we can stop checking after \(\sqrt{16}\), which is 4. When x=36, we stop checking after \(\sqrt{36}\), which is 6. Here is the updated function with this addition:

# import for square root function
import numpy as np

def is_prime(x):

  if type(x) != int or x<2:
    return False   

  max_int = int(np.sqrt(x)+1)
  for n in list(range(2, max_int)):
    if  x%n == 0:
      return False

  return True

is_prime(7)

Output:

True

It’s a small change, but it effectively halves the number of calculations when solving for a prime number, which becomes exponentially more efficient as the numbers get larger and larger.

The method above works well when determining if a given number x is prime, but what if we want to find all the prime numbers up to a given number x? In this instance, if x=20, we want a function that will return all primes: 2, 3, 5, 7, 11, 13, 17, 19.

We could use the same function from earlier by simply creating a for loop that checks if each number up to x is prime. For example:

def prime_list_generator(x):

  prime_list = []
  for number in list(range(2, x+1)):
    if is_prime(number):
      prime_list.append(number)

  return prime_list

prime_list_generator(20)

Output:

[2, 3, 5, 7, 11, 13, 17, 19]

Great, it works! But this is terribly inefficient. There are a lot of repetitive and unnecessary steps since the function has to individually check every number in the list and perform many calculations to determine if each is prime. How can we solve for primes without having to prove each number up to x is prime?

One answer lies in the Sieve of Eratosthenes, an algorithm first referenced in the 2nd Century CE Ancient Greek text Introduction to Algebra and attributed to Eratosthenes of Cyrene, a Greek mathematician from the 3rd Century BCE.

Note: this is not the only ‘prime sieve’ to exist. In fact, there are a number of sieves that have been developed that are even more effective than the Sieve of Eratosthenes, but Eratosthenes’ is one of the most straightforward, so it is perfect for our current purpose.

This method functions in a seemingly backwards fashion. Instead of identifying all the prime numbers up to a given number x, the Sieve of Eratosthenes identifies all the composite numbers and removes them, leaving only the prime numbers. Though this seems backwards, it turns out that identifying composities is a lot easier than identifying primes. If we think back to our earlier attempts, we can see why this is.

When determining if x is prime, we first had to divide x by every smaller integer betweeen 2 and x. Even after our improvement of using \(\sqrt{x}\) instead of x, there are still a lot of calculations that need to be performed before we can verify that x is prime, and the number of calculations increases exponentially as x increases.

On the other hand, how easy is it to determine if a given number is not prime? The answer, as it turns out, is very easy. One way is to simply find all the multiples of each prime number, starting with 2. We can eliminate the multiples since they can’t be prime if they are divisible by 2. So with a minimal number of calculations, we have effectively removed half of the possible numbers from consideration (all even numbers). The next remaining number in the list of possible primes is 3. So we then remove all multiples of 3. The next remaining number is 5, because 4 was removed from consideration as it was a multiple of 2. We repeat this process up to \(\sqrt{x}\) until we have removed all composite numbers, leaving only the primes. Visually, it looks like this:

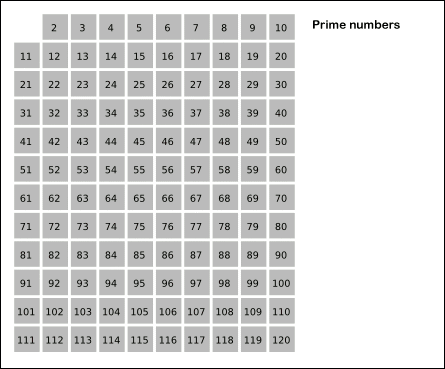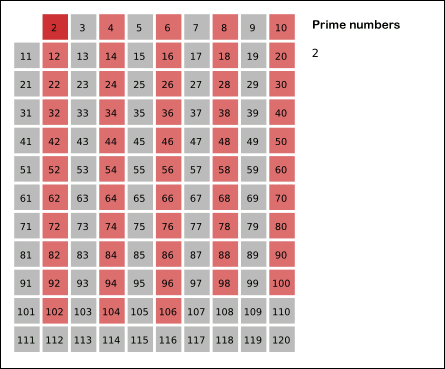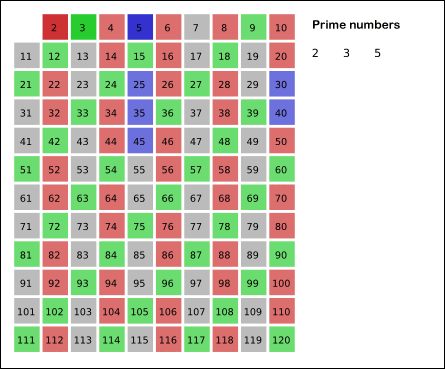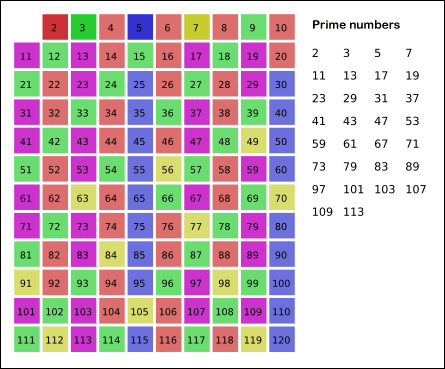Sieve_of_Eratosthenes_animation By SKopp at German Wikipedia

Now that we understand how the sieve works, we need to put it into code. In order to do this, I will:

  • create a list of numbers from 2 to x.
  • starting at 2, remove all multiples of each prime from the list
  • repeat up to the value of \(\sqrt{x}\)
def sieve_of_eratosthenes(x):
 # list of possible primes
 prime_list = list(range(2, x+1))
 p = 2
 # stop checking at sqrt(x)
 while p*p <= x:
   for i in range(p*p, x+1, p):
     if i in prime_list:
       prime_list.remove(i)
    p += 1

 return prime_list

sieve_of_eratosthenes(30)

Output:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

Excellent! We now have a way to return all prime numbers up to a given number x. I will leave you with one final version. This next version of the sieve is slightly more optimized, but also more complex. It uses a boolean array of True values instead of storing each integer. At the index location of each composite number, the boolean is changed to False. I can then use the index location of the remaining True values to find all the prime numbers. In order to do this, I will:

  • create a boolean array of length x-2 all set to True.
  • starting at 2, set all multiples of each prime equal to False
  • repeat up to the value of \(\sqrt{x}\)
  • the remaining True values are all prime numbers

Using a boolean array is faster and more efficient than performing operations on a list of numbers (especially as x increases), but as you can see, the code is more abstracted and not as immediately comprehensible.

def sieve_optimized(x):

  bool_list = [True for i in range(2, x+1)]
  prime_list = []
  p = 2

  while p*p <= x:
    if bool_list[p] is True:
      for i in range (p*p, x+1, p):
        prime_list[i] = False
    p += 1

  for i in range(2, x):
    if bool_list[i]:
      prime_list.append(1)

  return prime_list

sieve_optimized(30)

Output:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]

We have now covered many of the ways in which you can solve for prime numbers using Python. There are a multitude of other methods, however, and lots of small optimizations that I have not covered. If you have other methods of solving for primes I’d love to hear them. As I mentioned, there are also lots of other more complex prime sieves. If this is something you’d like to hear more about, let me know. I’d love to do another dive into more complex prime methods.

You May Also Enjoy